% Author: JONAH KADOKO % Tufts University % Numerical Methods (ES 55) FINAL PROJECT (Nov 2 2011) % % The purpose of this program is to simulate the dynamics of a wheelchair at % given parameters: namely, Mass of rider, road profile, force of % propulsion, bearing frictional torque, and wheelchair dimensions. % The main figure of the program will plot a wheelchair moving along a % user-defined road. The user can choose to plot energy, distance, speed % and jerk graphs by clicking buttons on the main figure to the left. % The following are the required files: % wheelchair1.m - function that carries the differential equation % governing dynamics of wheelchair. Essential. % PlotOther.m - script that plots results of energy,distance, velocity, % acceleration andjerk. Essential % road.m - function that calculates the (x,y) coordinates of road profile % as well as the curved distance along the road. Essential. % wCcalculations.m - function that calculates energy, distance etc from % the output of ODE23. Essential. % endEvent.m - function for ending ODE23 solver. Essential. % wC.mat - (x,y) coordinates of wheelchair drawing. Important if the user % desires a visually appealing animation. Less Essential. % [importing_jpg_for_xy_points.m] - script for importing jpeg picture to % (x,y) coordinates. This file is not needed unless the user % wants to modify the wheelchairpicture % [animaition.avi] - animation vedio, this is optional. Uncomment % VideoWriter() line and mov() lines clear;close all; addpath('C:\Users\Jonah\Documents\ES 55\Final Project\Matlab files'); % Parameters of the wheelchair/rider Mw=5; % Mass of back wheel (kg) theta=[-180 20]; % initial position of and speed of wheelchair [rad rad/s] Rp=0.4; % radius of the push ring (m) Rbw=0.5; % radius of the back wheel (m) Mr=100; % Mass of rider in kg F=100; % force input +by the rider (N) k=1; % frictional coefficient of bearings (greater than 1 is fine) dt=0.1; % size of time steps (s) tMax=300; % the time to simulate (s) T=5; % time it takes for the rider to put more force (s) % road variables xMax=500; % the maximum amount of distance to be travelled by the rider % (x.^3)*(-0.010)+x.^2*0.5 - Potential candidate for road profile (m) % rdFunc=@(x) exp(-.001*x).*sin(0.01*x); % road profile function (m) [xRd,yRd,s]=road(rdFunc,xMax); % x,y coordinates of road (m) [nxRd,nyRd,ns]=road(rdFunc,-xMax); % calculating behind the starting point s=[ns s];xRd=[nxRd xRd];yRd=[nyRd yRd]; % Differential equation governing the dynamics of the wheelchair tspan=0:dt:tMax; options=odeset('events',@endEvent); % set the end conditions [t,Ang]=ode23(@wheelchair1,tspan,theta,options,xRd,yRd,s,F,Rp,Rbw,Mw,Mr,k,T); yMax=max(yRd);yMin=min(yRd); % Calculations of Energy, Displacement, Speed, [kE,pE,tE,dispXY,dispX,dispY,dist,v,Acc,Jerk]=wCcalculations(t,Ang,F,Rbw,Mr,Mw,s,xRd,yRd,dt); load wC % load the coordinates of the picture of wheelchair. I drew this % picture using CAD software and then extracted the (x,y) coordinates using % MATLAB. Feel free to replace wC with custom picture. % Define the limits of the graphs screenSize=get(0,'ScreenSize');plotW=0; GUI=figure('Position',screenSize,'Name','WheelChair Simulation Window','NumberTitle','off'); % animation variables % This feature is not present in some versions of MATLAB % mov=VideoWriter('animationES55.avi');mov.FrameRate=10;open(mov); % Define the limits of the graphs d=1e-2; % this is the duration of one frame fSize=16; % Font size wchair=wC;Rw_anim=1; nChair=length(wchair);% wheel chair figure dispMax=max(dispXY);dispMin=min(dispXY); vMin=min(v); vMax=max(v); tMax=max(t); % maximum time % Road Animation Limits if yMax <5,yMax=5; end if yMin>-5, yMin=-5; end % WheelChair Parameters Lmin=min(wC(:,1));Lmax=max(wC(:,1));%Length limits of the wheelchair Hmin=min(wC(:,2));Hmax=max(wC(:,2));%Height limits of wheelchair sX=0.1*xMax/(Lmax-Lmin); % calculating the scale factor in X sY=0.2*(yMax-yMin)/(Hmax-Hmin); % calculating the scale factor in Y wC=[sX*wC(:,1) sY*wC(:,2)]; % scale wheel chair and ... % Translate the wheel chair to start at origin % the frontWheel min is at row = 3882 % The backWheel min is at row = 2323 bkWheelMin=[wC(2323,1),wC(2323,2)];frWheelMin=[wC(3882,1),wC(3882,2)]; Lmin=min(wC(:,1));Lmax=max(wC(:,1));L=abs(bkWheelMin(1)-frWheelMin(1)); wC=wC+repmat([-bkWheelMin(1) -bkWheelMin(2)],nChair,1); bkWheelMin=[wC(2323,1),wC(2323,2)];frWheelMin=[wC(3882,1),wC(3882,2)]; rot=eye(2); % this is the rotation matrix for the wheelchair (not using it) % SET GUI controls runButton=uicontrol('style','pushbutton','string','RUN',... 'position',[25 600 90 50],'callback','Final_Project_mainscript_JonahKadoko;'); plotEnergy=uicontrol('style','pushbutton','string','Plot pE,kE & dist',... 'position',[25 500 90 50],'callback','PlotOther;plotW=1;'); plotVel=uicontrol('style','pushbutton','string','Plot v, & Acc',... 'position',[25 400 90 50],'callback','PlotOther;plotW=2;'); plotJerk=uicontrol('style','pushbutton','string','Plot Jerk;',... 'position',[25 300 90 50],'callback','PlotOther;plotW=3;'); % Loop through every frame for frame=1:length(Ang) % calculate the intersection of the wheel chair front wheels with road % My idea was to rotate the orientation of wheel chair with the slope of % the road. It worked fine except that the sloped wheelchair is not % visually appealing. I will work on that in future versions. % theta=intersection(rdFunc,bkWheelY,bkWheelX,L); % rot=[cos(theta) sin(theta); % -sin(theta) cos(theta)]; % move and rotate the wheel chair wchair=repmat([dispX(frame) dispY(frame)],nChair,1)+wC*rot; % plot the wheelchair plot(wchair(:,1),wchair(:,2),'o','MarkerSize',Rw_anim);hold on; % draw the road plot(xRd,yRd,'m','LineWidth',3); title('Animation of Wheel Chair','FontSize',fSize,'FontWeight','bold'); xlabel('x (m)','FontSize',fSize,'FontWeight','bold'); ylabel('z (m)','FontSize',fSize,'FontWeight','bold');hold off; axis([-1.3*xMax xMax yMin 0.4*(yMax-yMin)+yMax]); % axis([dispMin*Rbw dispMax*Rbw 0 10]); % Write the video file. This feature is not available in some MATLAB % versions. % frame=getframe(GUI,screenSize); % writeVideo(mov,frame); pause(d); end % close(mov);

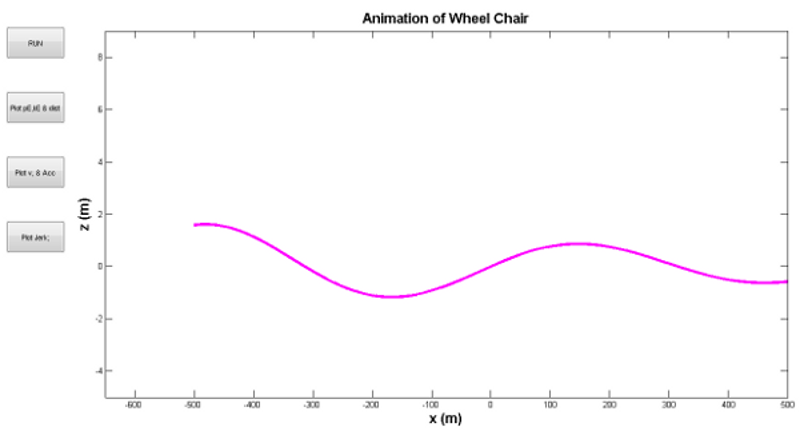
Results
I verified my math with the math in this paper and I found it to be realistic.