Packing Circles in a Big Circle

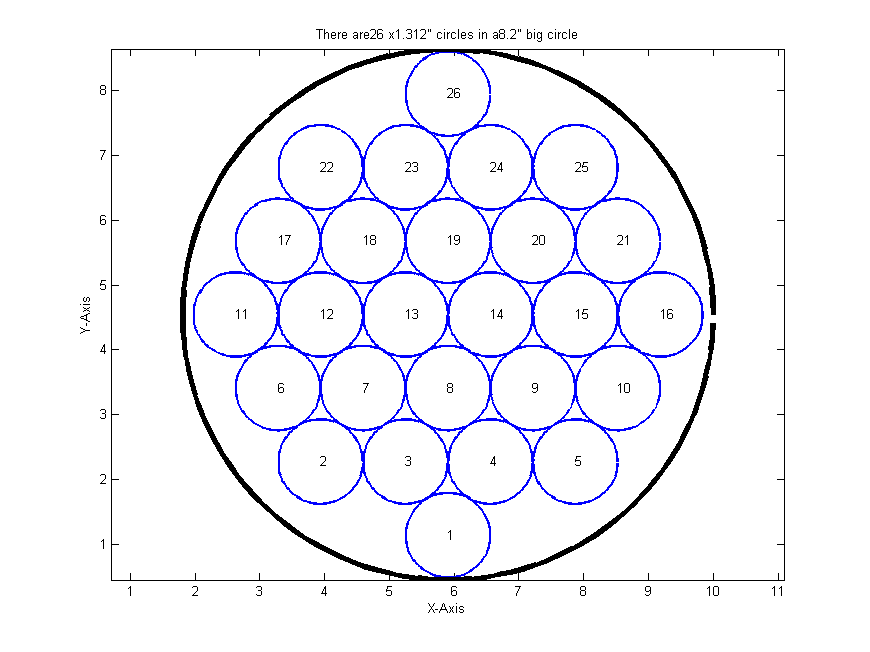
packingCirclesNCircle_For_PracticalPurposes

How many 1.23″ circles can you pack in an 8.5″? You have 2 mins to solve…

The problem statement is,’ How many circles can you pack in one big circle?’. It may sound like a trivial problem, but when you sit down to solve it, you quickly realize that it isn’t. I learned from experience the night I did this sub-project.

Why did I bother doing this? Well, I needed to figure out an approximate number of ‘circles’ that could fit in a ‘big circle’ so I can go ahead with main design project. In this case, ‘small circles’ can be electrical cables and the ‘big circle’ can be a conduit, raceway, or a sheath.

In electrical installations, the quantity of electrical cables pulled through a conduit is determined by the relevant NEC (National Electric Code) section. (image from www.ecmweb.com)

Without a solution like the one described herein, I resorted to good old SolidWorks to quickly pattern small circles, fit one large circle and then count the little ones. This approach works when you want to estimate a small number of ‘circles’, as the population increases, SolidWorks may start to run into graphics issues because of too many sketches.

I did find a few academic algorithms/formulas in literature, but I didn’t have the luxury of reading long mathy papers. However, there were some industrial solutions that I found. For example, for packing cables in cylindrical conduit in the solar/electrical industry, the National Electric Code has pre-calculated results that only work for a given combinations of wire sizes and fill-factors. I didn’t have a fill factor in mind nor did I want one: I needed to see visually what the result looks like.

In conclusion, to the best of my searches at the time, there wasn’t a tool/easy solution to do this so I decided to make my own. My solution is pretty easy to follow as I commented step-by-step in the following code.

The code

%AUTHOR: JONAH KADOKO
% 1/26/13

% THIS PROGRAM SOLVES FOR THE NUMBER OF CIRCULAR OBJECTS ONE CAN FIT IN A
% BIG CIRCLE

% SCOPE:
% 1. THIS PROGRAM HAS NOT BEEN OPTIMIZED TO FIND MAXIMUM NUMBER OF
% SMALL CIRCLES.
% 2. THIS PROGRAM IS RECOMMENDED FOR USE BY PEOPLE TO ESTIMATE THE NUMBER
% OF CIRCULAR OBJECTS IN PRACTICAL APPLICATIONS.


clear all;close all;
% User Variables:
d=1.312; % diameter of the small circles
D=8.2; % diameter of the big circle
% there is some round off error, play around with D or d to get a sweet
% spot

% Internal Variables:
r=d*0.5; % radius of small circles
R=D*0.5; % radius of the big circle
rot_R=2*r; % radius from the center of the big circle
deltaY=sqrt((2*r)^2-r^2); % the vertical distance between adjacent
% small circles
ang=0:0.05:2*pi; % for plotting circles
xC=r*cos(ang);yC=r*sin(ang);
XC=R*cos(ang);YC=R*sin(ang);
% MAIN ALGORITHM

% 1. Solve for the number of circles that can be arranged
% straight in a row.
% Also equal to the longest row of circles in a hexagon
nRowMax=floor(R/r);
if mod(nRowMax,2)
    %     odd
    nRowMax=nRowMax+2;
    bigCirclePos(1,2)=0.5*(nRowMax-1)*deltaY;
    bigCirclePos(1,1)=(nRowMax-1)*r;
else
    %     even
    nRowMax=nRowMax+2;
    bigCirclePos(1,2)=0.5*nRowMax*deltaY;
    bigCirclePos(1,1)=(nRowMax+1)*r;
end

% 2. Draw circles in a big square
% 3. Weed-out small circles that do NOT
CircleTempPos=zeros(nRowMax^2,2);
nSquare=0;nCircle=0;nonCircle=0;

for row=1:nRowMax
    for col=1:nRowMax
        nSquare=nSquare+1;
          %       for all even rows, an offset of r is applied
        CircleTempPos(nSquare,1)=(col-1)*2*r+(1+(-1)^(row))*0.5*r;
        CircleTempPos(nSquare,2)=(row-1)*deltaY;
        rot_R=sqrt((CircleTempPos(nSquare,1)-bigCirclePos(1,1))^2+...
            (CircleTempPos(nSquare,2)-bigCirclePos(1,2))^2)+r;
        if rot_R<=R
            nCircle=nCircle+1;
            inscribedCircle(nCircle,:)=CircleTempPos(nSquare,:);
        else
            nonCircle=nonCircle+1;
            nonInscribedCircle(nonCircle,:)=CircleTempPos(nSquare,:);
        end
    end
end

figure(1)
%  4. Plot circles, that fit and those that do not
% solve xy position of circles

% a) small circles that fit
for n=1:nCircle
    plot(inscribedCircle(n,1)+xC,inscribedCircle(n,2)+yC,'b',...
        'LineWidth',2);
    hold on
%     plot(inscribedCircle(n,1),inscribedCircle(n,2),'ob');
    text(inscribedCircle(n,1),inscribedCircle(n,2),num2str(n));

end
% b) big circle

plot(bigCirclePos(1,1)+XC,bigCirclePos(1,2)+YC,'k','LineWidth',4);
% plot(bigCirclePos(1,1),bigCirclePos(1,2),'ok');
% c) circles that do not fit

% plot(nonInscribedCircle(:,1),nonInscribedCircle(:,2),'or',...
%     'MarkerSize',5,'MarkerFaceColor','r')

title(strcat('There are ',num2str(nCircle),' x ',num2str(d),...
    '" circles in a ',num2str(D),'" big circle'))
xlabel('X-Axis')
ylabel('Y-Axis')
hold off
axis equal
packingCirclesNCircle_For_PracticalPurposes

The result of my code

Published with MATLAB® 7.8

CAD, Matlab, Past Projects, Software